Lösungen Kapitel 35

From BioPhy.de Wiki

Aufgabe 35.1:

Wie man ebene Kristalle durch Kombinationen von Disklinationen aufrauen kann.

Vorbemerkung und Definitionen: Versetzungen und Disklinationen spielen in der Natur immer dann eine wichtige Rolle, wenn flüssig-kristalline Filme (wie Membranen) und zweidimensionale Kristalle gekrümmt werden müssen, Beispiele sind die Bildung von Vesikeln aus Lipiden in einer Gel-Phase (P $LaTeX: _\beta$ und L $LaTeX: _\beta$ , Kapitel 10 bis 12) und die Schalen der Viren. Disklinationen spielen eine besonders wichtige Rolle, wenn die Lipidketten gegenüber der Membrannormale geneigt sind, wie im Fall der P $LaTeX: _\beta$ - Phase (siehe auch [4]). Wie im Kapitel 12.3 gezeigt wurde, können Disklinationen oder andere Defekte enzymatische Reaktionen in Biomembranen kontrollieren.

Abb.1: a) Erzeugung von $LaTeX: \pm 60$ \degree Disklinationen durch Ausschneiden bzw. Einfügen von 60\degree-Keilen. b) Oben: Form eines ebenen Kristalls mit einer -60\degree (links) und einer +60\degree Disklination (rechts). Die Bilder stammen aus der Arbeit von Seung und Nelson [1]). Sie zeigen, dass die Kristallplättchen nach der Vereinigung der Ränder der Schnitte stark deformiert werden. Die Kristallebenen werden stark nach außen oder innen gebogen. Das untere Bild zeigt anschaulich, dass die Deformation der Kristallebenen (und damit der elastische Energieaufwand) wesentlich reduziert wird. c) Bildung von Schraubenversetzung in einem Vesikel im kristallinen Zustand L $LaTeX: _\beta$ (s. Kapitel 10. 2). Man beachte, dass die Spitze die Form eines Zwiebelturmes hat. Ursache ist Neigung der Ketten gegenüber der Membran-Normalen [2]. Durch Bildung der Hutspitze ändert sich die Orientierung der Lipidketten kontinuierlich.

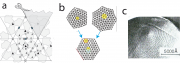
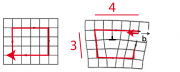
Unter Versetzungen (engl. dislocation) versteht man Defekte in der Ordnung der Positionen der Moleküle oder Atome. In einem 2D-Kristall mit hexagonaler Gitterstruktur erzeugt man z.B. eine Stufenversetzung durch Einschub einer zusätzlichen Kristallebene (s. Abb. 1b unten).

Unter Disklinationen in 2D-Kristallen versteht man Störungen in der Orientierung der Kristallebenen (wie in Abb. 1b oben gezeigt). Der Begriff kommt eigentlich aus der Physik der Flüssigkristalle, deren molekulare Ordnung durch die mittlere Orientierung der Moleküle (den 'Direktor') bestimmt ist. In diesem Fall versteht man unter Disklinationen die abrupte Änderung der mittleren Molekülorientierung wenn Bereiche verschiedener Richtungen des Direktors aneinander stoßen. Sie sind mit einem Aufwand an elastische Energie verbunden.

Wie in der folgenden Aufgabe gezeigt wird, ist der Aufwand an elastischer Energie zur Bildung von Disklinationen in 2D-Kristallen sehr hoch und wächst mit der Größe des Kristalls stark an. Wie Abb. 1b anschaulich zeigt, kann diese Energie durch Bildung von Paaren von +60 \degree - und -60 \degree - Disklinationen wesentlich reduziert werden, unter Erhalt der ebenen Struktur. Man erkennt leicht, dass ein solches Paar mit einer Stufenversetzung identisch ist.

Eine andere Möglichkeit ist die in Kapitel 35 ausführlich beschriebene Bildung gekrümmter Kristalle. Durch Kombination von Disklinationen verschiedener Vorzeichen entstehen wellenförmige Oberflächenprofile (s. Abb. 35. 7). Je höher die Zahl solcher Paare von Disklinationen ist, umso flacher kann eine makroskopische Platte werden. Man beachte auch, dass man von den ebenen Kristallen mit vielen Stufenversetzungen zu rauen Platten übergehen kann, indem die Paare von Disklinationen der Versetzungen disoziieren [1].

Paare von Disklinationen verschiedener Vorzeichen haben große Ähnlichkeit mit elektrischen Dipolen.

Referenzen:

1 Seung H.S. Nelson D.(1988) Defects in flexible membranes with crystalline order. Phys. Rev, A 38: 1005-1018.

2 E.Sackmann 'Physical basis of self organization and function of membranes. Physics of vesicles. in Handbook of Biological Physics' Ch.V,(eds. R. Lipowsky und E. Sackmann. Elsevier Amsterdam 1995.

Gebhardt, C., Gruler, H., Sackmann, E. (1977) On domains structure and and local curvature of lipid bilayers. Zeitschrift für Naturforschung 32.c: 581-596

Rüppel, D., Sackmann, E., (1983) On defects in different phases of two-dimensional lipid bilayers. J. de Physiques 44: 1025-1034

Aufgabe 35.2:

Vergleich der Energien von Disklinationen und Versetzungen-Hexatische Phasen.

Einleitung: Die Versetzungen werden durch den Burgersvektor b charakterisiert. Man erhält diesen, indem man um eine Versetzung herum läuft und die Weglänge L bestimmt, wobei die Schrittlänge $LaTeX: \delta u$ gleich der Gitterkonstanten a ist. Der Betrag des Vektors, |b|, ist gleich der Differenz der Weglängen $LaTeX: L_0-L$ , wobei $LaTeX: L_0$ die Weglänge ist, die man erhält, wenn man im gleichen Abstand um einen normalen Gitterpunkt herum läuft. Der Burgersvektor ist das Integral über alle Schritte $LaTeX: \vec{b}=- \oint \delta \vec{u_i}$ und ist ein Maß für die Deformation des Gitters durch die Versetzung [1]. Der Betrag des Burgersvektors ist von der Größenordnung der Gitterkonstanten a.

Abb. 1: Zur Definition des Burgersvektors.

Die Energie einer Versetzung in einem 2D Kristall hängt logarithmisch von dessen Durchmesser d=2R ab:

$LaTeX: W_{disloc}=Yb^2ln(\frac{R}{a})$

wobei Y der Kompressionsmodul eines 2D-Gitters ist. Diese elastische Energie wird jedoch durch die Translations-Entropie reduziert. Diese ist durch die Zahl möglicher Verteilungen einer Versetzung in dem Kristall bestimmt und hat die Form $LaTeX: \delta S= 2k_BTln(\frac{R}{a})$ . Erhöht man die Temperatur auf $LaTeX: T>T_m= \frac{Yb^2}{k_B}$ , so wird die Entropie größer als die elastische Energie. Dies führt zu einer lawinenartigen Zunahme der Zahl der Versetzungen bei $LaTeX: T_m$ und die Ordnung des Kristalls wird (wie beim Schmelzen) zerstört.

Tatsächlich wird zuerst nur die kristalline Anordnung (die Fernordnung) der Moleküle zerstört, während die weitreichende Orientierung der ursprünglichen Kristallebenen noch erhalten bleibt. Es entsteht ein neuer Zwischenzustand, in der die globale Ordnung der Orientierung der Kristallebene (die sog. Fernordnung) erhalten bleibt, während die Fernordnung der Position der Moleküle zerstört wird. Man nennt solche Zustände der Materie hexatische Phasen [2].

Die Betrachtung der Abb.1b in Aufgabe 1 zeigt, dass die Kristalle durch isolierte Disklinationen sehr viel stärker deformiert werden als durch Versetzungen. Tatsächlich hängt die zur Erzeugung einer Disklination notwendige elastische Energie quadratisch von der Größe d = 2R des Kristalls ab:

$LaTeX: W_{disclin} =Ys^2 R^2$

wobei s die 'Ladung' der Disklination ist. s ist gleich dem Winkel des in den Kristall eingesetzten oder aus diesem ausgeschnittenen Stücks (s. Aufgabe 36.1 Abb. 1a), gemessen in Radians. 60\degree Disklinationen haben die Ladungen $LaTeX: \pm\frac{2\pi}{3}$ .

Berechnung der Energien für:

1) Vesikel: Durchmesser: $LaTeX: \phi=1 \mu m$ , $LaTeX: b \approx a=1 nm$ , $LaTeX: Y= 0.700\frac{N}{m}$ . Die elastische Energie der Versetzung: $LaTeX: W_{disloc} \approx 500 k_BT$ . Die elastische Energie der Disklination: $LaTeX: W_{disclin} \approx 10^8 k_BT$ . Die Translationsentropie ist $LaTeX: \Delta S \approx 7 k_BT$ . Man beachte: der Wert $LaTeX: Y=0.7 \frac{N}{m}$ gilt für 1:1 DMPC-Cholesterol Mischungen. Für Vesikel aus reinem DMPC wird $LaTeX: Y=0.15 \frac{N}{m}$ und $LaTeX: W_{diloc}$ wird um den Faktor 5 reduziert. Die elastische Energie der Defekte kann durch Einbau von kleinen Molekülen oder Proteinen wesentlich reduziert werden, wie in Kapitel 12 oder [3] gezeigt wird.

2) Viren: Durchmesser: $LaTeX: \phi=0.1 \mu m$ , $LaTeX: b \approx a=10 nm$ , $LaTeX: Y= 1 \frac{N}{m}$ . Die elastische Energie der Versetzung: $LaTeX: W_{disloc} \approx 5 \cdot 10^4 k_BT$ . Die elastische Energie der Disklination: $LaTeX: W_{disclin}\approx 2.5 \cdot 10^6 k_BT$ . Die Translationsentropie ist $LaTeX: \Delta S \approx 4.6 k_BT$ . Wie in diesem Kapitel gezeigt wurde, wird die sehr große Energie der Disklination durch Bildung von Icosaedern wesentlich reduziert. Daher behindern sie die Selbstassemblierung der Hüllen der Viren nicht. Außerdem gelten die obigen Werte für die reifen Viren , während frisch gebildete Hüllen zahlreiche lokale Defekte aufweisen.

Referenzen:

1 Landau, LD., Lifshitz, EM. Theoretische Physik VII Elastizitätstheorie

2 Seung H.S. Nelson D.(1988) Defects in flexible membranes with crystalline order. Phys. Rev, A 38: 1005-1018.

3 E.Sackmann 'Physical basis of self organization and function of membranes. Physics of vesicles. in Handbook of Biological Physics' Ch.V,(eds. R. Lipowsky und E. Sackmann. Elsevier Amsterdam 1995.

Aufgabe 35.3:

Die Federkonstante der Viren.

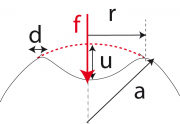
(Siehe auch Frage 11.2) Wir betrachten eine Kugel mit dem Radius a. Die Berechnung der Federkonstante basiert auf der Idee, dass die elastische Energie durch die Deformation am Rand L bestimmt ist, da dieser die größte Krümmung aufweist [1]. Der Rand habe den Radius r. Die Deformation der Eindellung und der Schale außerhalb des Randes wird vernachlässigt.

Daher sind die lokale Biegedeformation bzw. die Dehnung von der Größenordnung $LaTeX: \frac{\partial^2 u}{\partial x^2} \propto \frac{u}{d^2}$ bzw. $LaTeX: \frac{\Delta A}{A} \approx (\frac{u}{a})^2$ . Die Dehnungs- und Biegeenergie werden daher:

$LaTeX: G_d \approx d^2K(\frac{u}{a})^2$ und $LaTeX: G_b \approx d^2 \kappa (\frac{u}{d^2})^2$ (1)

Nach Kapitel 12 ist $LaTeX: \kappa \approx Eh^3$ und der Flächen-Kompressionsmodul $LaTeX: K \approx Eh$ , wobei h die Dicke der Schale ist.

Aus der Bedingung, dass die Gesamtenergie ein Minimum sein muß, erhält man für die Breite des Deformationsbereichs $LaTeX: d^2=ha$ , wie man leicht nachvollziehen kann. Mit dieser Beziehung wird die Gesamtenergie:

$LaTeX: \Delta G=G_b +G_d = 2\frac{Eh^2 u^2}{a}$ (2)

Nun ist die Kraft gleich der Variation von $LaTeX: \Delta G$ bezüglich u und daher wird

$LaTeX: f\approx (\frac{Eh^2}{R})u$

Dies entspricht der Kraft-Dehnungs-Beziehung einer Feder mit der Federkonstanten $LaTeX: k=\frac{Eh^2}{R}$ .

Um k als Funktion der elastischen Module auszudrücken, kann man die Membrandicke eliminieren, indem man die Beziehung $LaTeX: Eh= \sqrt{\kappa K}$ benutzt.

Abb.1: Eindellung in einer Kugelschale durch eine Punktkraft f. Die elastische Energie ist durch die starke Krümmung am Rande der Eindellung dominiert. Diese hat die Breite d.

Referenz:

1 Landau, LD.,und Lifschitz, EM. 'Lehrbuch der Theoretischen Physik Vol VII. Elastizitätstheorie' Akademie-Verlag, Berlin 1983

Aufgabe 35.4:

Strukturbestimmung der Viren mittels SANS und SAXS:

Da die SANS und SAXS ähnliche Information liefern, beschränken wir uns auf die erste Methode. Die wesentlichen Grundlagen der Kleinwinkelstreuung wurden in Appendix 37. A zusammengestellt. Dort wurde gezeigt, dass die Information über die Struktur der Viren aus dem Strukturfaktor f(q) oder der gestreuten Intensität I(q) erhalten wird. Der Strukturfaktor für Objekte mit sphärischer Symmetrie hat die Form (siehe [1, 2] und Appendix 37.A):

$LaTeX: f(q)=4\pi\int_0^R\rho(r) \frac{sin(qr)}{qr}r^2$ (37A.5)

Die Methoden eignen sich besonders zur Untersuchung der Modifikation der Virenschalen während der Reifung. Wie wir bei der Diskussion der Reifung der Viren sahen, wird das Capsid oft durch Gerüstproteine stabilisiert, bis diese Rolle durch die RNA oder DNA übernommen wird. Eine elegante Untersuchung von D. Kuzmanovic et al [3] zeigt, welche wichtige Information über die Struktur der Schalen und deren Änderung vor und nach der Injektion der RNA aus SANS Untersuchung gewonnen werden kann.

In dem Experiment wurde die Struktur von Bakteriophagen des Stamms MS2 (die E. coli Bakterien angreifen) untersucht. Die Hülle besteht aus drei nahezu gleichen Proteinen mit MG~14 kDa. Sie wird während der Assemblierung und vor dem Einbau der RNA (in [3] 'pre infection state' genannt) zusätzlich durch ein Gerüstprotein mit 44kDa ('Protein A' genannt) stabilisiert. Nach der Injektion der RNA in die Wirtszelle trennt sich das A Protein von der Hülle und man nennt den Zustand 'post infection' state. In dem Experiment wurde die Struktur der Hülle mit und ohne A-Protein aufgeklärt und die Wirkung der RNA auf die Struktur der Hülle analysiert. Wir beschreiben zunächst ein wichtiges Ergebnis der Experimente und ziehen dann wichtige Konsequenzen aus der Arbeit von Kuzmanovic et al [3].

Theoretische Grundlagen der Analyse der SANS von Schalen.

Man kann die Streuintensität einer Suspension dünner Kugelschalen (wie Vesikel oder vom Genom befreite Viren) durch Erweiterung des Guinier-Porod Modells berechnen. Bei der Strukturbestimmung intakter Viren kann man den Beitrag der RNA auszublenden, indem man dessen Kontrast, durch partielle Deuterierung des Lösungsmittels, an den des Lösungsmittels anpasst. Nach Gl 37A.3 ist $LaTeX: I(q \rightarrow 0) = \Delta \rho V$ und man kann somit aus dem asymptotische Wert der Streuintensität die Masse der Teilchen bestimmen. Als nächstes nehmen wir an, dass die Schale aus zwei Kugeln mit Radien R1 und R1 aufgebaut sei. Sind die Dichten der Kugeln gleich, so hat die Streuamplitude die Form:

$LaTeX: f(q)=\frac{4\pi}{3}\Delta \rho (R_2^3f_2(q,R_2)-R_1^3f_1(q,R_1))$

wobei die Funktionen $LaTeX: f_i(q,R_i)$ durch Gleichung 37A.6 gegeben sind:

$LaTeX: f(q)=4\pi\int_0^R\rho(r) \frac{sin(qr)}{qr}r^2$ (37A.5a)

Die gestreute Intensität ist daher von der Form:

$LaTeX: I(q)= f(q)^2$ (37 A.5b)

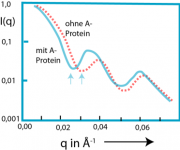
Abb. 1: Streuintensität I(q) der Virusschale mit (durchgezogene Linie) und ohne Helferprotein A (gestrichelte Kurve) nach [3]. Man beachte die Verschiebung der Minima zu kleineren q-Werten

Abb. 1 zeigt die SANS-Streukurve der Viren in Abwesenheit und Anwesenheit des Gerüstproteins A. Obwohl die Unterschiede der Streukurven nicht sehr groß sind, erkennt man deutlich, dass die Minima in Anwesenheit des A-Proteins zu kleineren q-Werten verschoben werden. Daraus folgt, dass die Schale dadurch dicker wird. Genauere Datenanalyse zeigt, dass die Schale durch das Gerüstprotein verdickt wird.

Die Ergebnisse der Strukturuntersuchung lassen sich wie folgt zusammenfassen:

1) Aus dem Guinier-Diagramm (logI(q) vs. q) kann man direkt den Gyrationsradius (zu 130 nm) bestimmen und aus I(0) erhält man (durch Extrapolation auf $LaTeX: q \rightarrow 0$ ) die Masse des Virus. Da man das Molekulargewicht der Capsidproteine kennt, erhält man die Zahl der Proteine pro Capsid. Da diese jedoch auch aus anderen Messungen bekannt ist, kann man nachprüfen, ob das Modell richtig ist.

2) Das wichtigste Ergebnis ist Folgendes: In Anwesenheit des A-Proteins hat die Schale eine Dicke zwischen 2.1 und 2.5 nm. Diese verdickt sich bei Entfernung des A-Proteins auf 3.1-3.7 nm. Der erstere Zustand (mit dünner Hülle) entspricht der Situation vor der Ejektion der RNA (d.h. vor der Infektion der Zellen). Die Schale verdickt sich nach der Entfernung des Genoms, da diese mit der Entfernung des Gerüstproteins A einher geht.

3) Die Dicke der Schale mit dem Stabilisator A wird durch den Einbau der RNA nicht geändert, sondern ist vor allem durch A bestimmt.

4) Die Rolle des Stabilisators A ist noch unklar. Möglicherweise induziert die Bindung des A-Proteins an die Innenseite der Hülle eine laterale Spannung in dem Capsid, das dadurch gestreckt und dünner wird. Die mit der mechanischen Spannung verbundene elastische Energie könnte zur treibenden Kraft für die RNA-Ejektion beitragen. Da die RNA mit dem A-Protein Komplexe bildet vermittelt dieses die Bindung des Genoms an die Innenseite der Schale. Möglicherweise induziert die Bindung des A-Proteins an die Innenseite der Hülle eine laterale Spannung des Capsids. Da diese die Bildung von Poren an den Ecken des Icosaders begünstigt, wird der Transfer der RNA durch die Poren der Hülle erleichtert [4].

Strukturbestimmungen mittels elektronenmikroskopischen Methoden.

Zur Erzeugung von Kontrast werden zwei Methode benutzt: Die Kryofixierung [5, 6] und die negativen Anfärbung (negative staining).

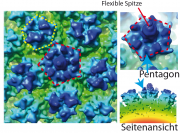
Abb. 2: Oben: Mit negative staining gewonnenes EM-Bild des Gurken-Mosaik-Virus. Unten: Bestimmung der Feinstruktur des Adenovirus mit 1 nm Auflösung mittels Kryo-Elektronenmikroskopie. Man erkennt den Aufbau aus pentameren und hexameren Capsomeren.

1. Bei der ersten Methode friert man die Proben so schnell ein, dass Wasser amorphes Eis bildet (sog. 'vitrified ice'), denn Mikrokristalle aus Eis würden die Beobachtung der Virenstruktur unmöglich machen. Um Strahlenschädigungen zu vermeiden, muss man bei sehr kleinen Elektronen-Intensitäten arbeiten, was sehr teuere Elektronenmikroskope erfordert. Man nimmt Bilder von sehr vielen Projektionen der in Eis eingebetteten Objekte auf und rekonstruiert die 3D-Struktur mit spezifischen Algorithmen. Man kann Auflösungen von 1 nm erhalten und auch die Struktur in Richtung senkrecht zur Oberfläche der Virenschalen bestimmen (s. Abb. 2b).

2. Bei der zweiten Methode wird die Struktur der Viren mit Schwermetall-Ionen Metallionen sichtbar gemacht. Diese lagern sich in Bereichen zwischen den Proteinkomplexen an und markieren so die Umrisse der Proteine. Man bestimmt so das Profil der Oberfläche mit einer Auflösung von 2 nm. Mit dieser Methode hat man erstmals entdeckt, dass kleine Viren aus Capsomeren mit pentagonaler und hexagonaler Symmetrie bestehen, was zum Bild der Icosaeder von Caspar und Klug führte.

Referenzen:

1 Svergun, D., Koch, M. (2003) Small-angle scattering studies of biological macromolecules in solution Rep. Prog. Phys. 66: 1735

2 G. Porod, Die Röntgenklemwinkelstreuung I. Z Naturforschung 134, 83 (1951)

3 D. Kuzmanovic et al (in J Mol. Biol 355, 1095-1111, (2006))

4 Deborah, A. et al. (2006) The MS2 Coat Protein Shell is Likely Assembled Under Tension: A novel role for the MS2 bacteriophage A protein as revealed by Small-angle Neutron Scattering. Journal of Molecular Biology, 355:1095-

5 Silvestry, M. et al. (2009) Cryo-Electron Microscopy Structure of Adenovirus Type 2. Temperature-sensitive mutant 1 reveals insight into the cell entry defect. Journal of Virology 83: 7375-

6 Conway, JF. et al. (2001) Virus mutations involving large subunits rotations and local refolding. Science 92: 744-748.

Search

Navigation

SEARCH

TOOLBOX

LANGUAGES

Lösungen Kapitel 35

From BioPhy.de Wiki

Contents

Aufgabe 35.1:

Aufgabe 35.2:

Aufgabe 35.3:

Aufgabe 35.4:

Toolbox